基于梯度的优化方法

我们把要最小化或最大化的函数称为目标函数或准则函数。

多维函数的偏导数

• 二元函数：$f(x, y)$
  $\frac{\partial f}{\partial x}$：f对x的偏导数，描述固定y时函数值f随x的变化率。
  $\frac{\partial f}{\partial y}$：f对y的偏导数，描述固定x时函数值f随y的变化率。
• 多维函数：$f:\mathbb{R}^n \rightarrow \mathbb{R}$，偏导数$\frac{\partial}{\partial x_i}f(x)$衡量点x处只有$x_i$增加时$f(x)$如何变化，$x=(x_1,x_2,...,x_n)$。

多维函数的梯度

• 二元函数：$f(x, y)$
  二元函数的梯度：{$\frac{\partial f}{\partial x}, \frac{\partial f}{\partial y}$}
• 多维函数：记为$∇_xf(x)$，梯度的第i个元素是f关于$x_i$的偏导数。
  $∇_xf(x)$ = {$\frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2},...,\frac{\partial f}{\partial x_n}$}

多维函数的方向导数

• 二元函数：$f(x, y)$
  
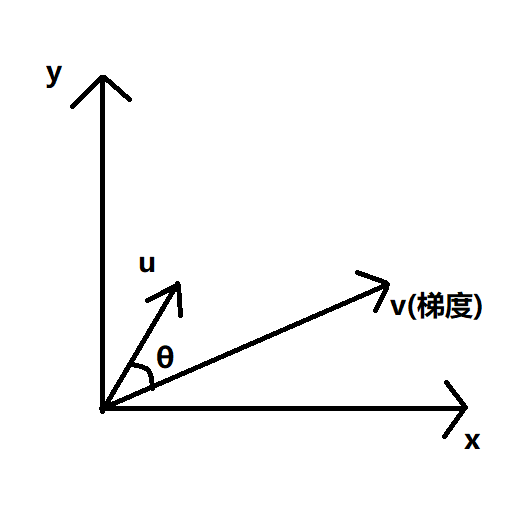
  其中v表示$f(x, y)$的梯度，u为单位向量。$f(x, y)$在u方向的方向导数，大小为v在u上的投影长度，方向为u。
  $\frac{\partial f(x)}{\partial x}\mid_u = u\cdot v$
• 多维函数：在多维情况下，
  $v = ∇_xf(x) \Rightarrow \frac{\partial f(x)}{\partial x}\mid_u = u^T∇_xf(x)$
  为了最小化$f$，希望找到使$f$下降的最快的方向，
  $\Delta f = \frac{\partial f(x)}{\partial x}\mid_u\cdot \Delta \Leftrightarrow \min \limits_{u,u^Tu=1}u^T∇_xf(x)$
  $= \min \limits_{u,u^Tu=1}\parallel u \parallel_2\parallel ∇_xf(x) \parallel_2\cos(\theta) \Leftrightarrow \min \limits_u \cos(\theta)$
  因此在u与梯度相反时，取得最小，称为梯度下降。梯度下降建议新的点为：
  $\hat{x} = x - \epsilon ∇_xf(x)$，其中$\epsilon$为学习率。

Jacobian和Hessian矩阵

有时需要计算输入和输出都为向量的函数的所有偏导数。如:
$f: \mathbb{R}^m \rightarrow \mathbb{R}^n$，则$f$的Jacobian矩阵$J \in \mathbb{R}^{n\times m}$为$J_{i,j} = \frac{\partial}{\partial x_j}f(x)_i$
例如：
$\begin{bmatrix} x \\ y \\ \end{bmatrix} \rightarrow \begin{bmatrix} 2x\sin(y) \\ y + 3x \\ \end{bmatrix}$
有时我们也需要计算二阶导数，二阶导数是对曲率的衡量，当函数有多维输入时，二阶导数也有很多，将其合并成一个矩阵，称为Hessian矩阵。
$H_{(f)}(x)_{i,j} = \frac{\partial^2}{\partial x_i \partial x_j}f(x)$
我们可以通过二阶导数预期一个梯度下降步骤能够表现的多好，在点$x^{(0)}$处作$f(x)$的近似二阶泰勒级数：
$f(x)\approx f(x^{(0)}) + (x - x^{(0)})^Tg + \frac{1}{2}(x - x^{(0)})^TH(x - x^{(0)})$，其中$g$是梯度，$H$是$x^{(0)}$点的Hessian。
当学习率为$\epsilon$，那么新的点$x$为$x^{(0)} - \epsilon g$，代入得：
$f(x^{(0)} - \epsilon g) \approx f(x^{(0)}) - \epsilon g^Tg + \frac{1}{2}\epsilon^2g^THg$
当$g^THg$为零或者负值时，近似的泰勒级数表明增加$\epsilon$将永远使$f$下降，但$\epsilon$很大的时候，泰勒级数的近似就不准确，因此需要更启发式的选择。
当$g^THg$为正时，使近似泰勒级数下降最多的最优步长为，
$\epsilon^* = \frac{g^Tg}{g^THg}$
最坏情况下，$g$与$H$最大特征值$\lambda_{max}$对应的特征向量对齐，则最优步长为$\frac{1}{\lambda_{max}}$，故在要最小化的函数能用二次函数很好近似时，Hessian矩阵的特征值决定了学习率的量级。

二阶导数测试

二阶导数可以用于确定一个临界点是否是局部极大点，局部极小点，或鞍点，但当$f''(x) = 0$时，测试是不确定的。
利用Hessian矩阵的特征值分解，可以将二阶导数测试扩展到多维情况，在临界点处($∇_xf(x) = 0$)，我们通过检测Hessian的特征值来判断该临界点是局部极大点，局部极小点，还是鞍点：

1. 若Hessian正定，则该临界点是局部极小值点。
2. 若Hessian负定，则该临界点是局部极大值点。
3. 当所有非零特征值是同号且至少有一个特征值为0时，检测不确定。

当$f(x)$在一个方向上导数增加很快，而在另一个方向上倒数增加很慢，此时梯度下降无法利用Hessian中的信息，不知道导数的这种变化，当函数呈长峡谷壮时，梯度下降法的效率极低。
我们可以利用Hessian矩阵的信息来指导搜索，解决这个问题，其中最简单的是牛顿法。
$f(x) \approx f(x^{(0)}) + (x - x^{(0)})∇_xf(x^{(0)}) + \frac{1}{2}(x - x^{(0)})^TH_{(f)}(x^{(0)})(x - x^{(0)})$
计算得临界点：
$x^* = x^{(0)} - H_{(f)}(x^{(0)})^{-1}∇_xf(x^{(0)})$

$Q = x^TAx$ $\frac{dQ}{dx} = 2Ax$ 基本思想：对x求导的结果要和x的形状相同。

只利用梯度信息的优化算法称为一阶优化算法，如梯度下降；利用Hessian矩阵的优化算法被称为二阶优化算法，如牛顿法。